Wintersemester 2014/15

(Pro-)Seminar zur diskreten Mathematik: Gitterpolygone

Dienstags 14-16
im SR 210, A3
Christian Haase

Um einen Eindruck von den Themen zu bekommen, mit denen wir uns beschäftigen werden, hier ein paar Knobelaufgaben.
Zeichnen Sie auf Karopapier ein konvexes Polygon mit allen Ecken an Karokreuzungspunkten. Ungefähr so:

Dabei bedeutet "konvex", dass man das Polygon entlanglaufen kann ohne links abzubiegen. Die beiden folgenden Bilder sind demnach verboten.

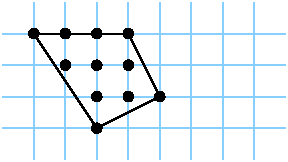
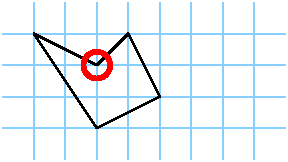
kein Kreuzungspunkt		nicht konvex

Für ein solches Polygon merken wir uns die Anzahl b der Karopapierkreuzungspunkte auf dem Rand, die Anzahl i der Karopapierkreuzungspunkte im Inneren sowie die eingeschlossene Fläche a, gemessen in Karopapierquadraten. Unser erstes Beispiel hatte (b,i,a)=(6,5,7).

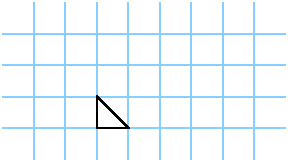
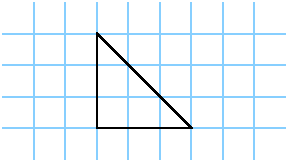
Spielen Sie mit diesen Figuren und finden Sie heraus, welche Tripel (b,i,a) Sie konstruieren können. Wenn ich also sage (3,0,1/2), zeichnen Sie das linke Bild,

                 

und wenn ich sage (9,1,4.5), zeichnen Sie das rechte Bild. Wie steht es mit (5,2,4)? (18,0,9)? (3,17,17.5)? (11,2,6.5)?

Spielregeln

• Sie halten einen ca. 60-minütigen Vortrag an den sich eine fachliche und didaktische Diskussion anschließen soll. Das Thema des Vortrags haben Sie sich -- selbstverständlich mit Hilfestellung -- weitgehend eigenständig erarbeitet.
• Sie schicken mir spätestens 4 Wochen vor Ihrem Vortrag (harte Deadline!) eine schriftliche Ausarbeitung (etwa 4 Seiten). Diese enthält die Struktur des Vortrags -- wann welche Definitionen, Beispiele, Resultate -- sowie Beweisideen.
• Anhand dieser Ausarbeitung besprechen wir gemeinsam Ihr Thema etwa 3-4 Wochen vor dem Vortrag. Sie sollten weitgehend die Inhalte verstanden und den Vortrag ausgearbeitet haben.
• Selbstverständlich sind Sie bei den anderen Vorträgen dabei und beteiligen sich bei der Diskussion.

Themen, Termine

Datum	Titel, Stichworte	SE/proSE	Referenz(en)	Vortragende(r)
14.10.	Hallo erstmal
21.10.	Polarität von Polygonen konvexe Hülle endlich vieler Punkte = beschränkte Lösungsmenge endlich vieler linearer Ungleichungen; Polarität "vertauscht" Ecken und Kanten.	SE	[JT, §§3.1-3.3, §5.3]	Felix Lorenz
28.10.	unimodulare Äquivalenz, HNF proSE unimodulare Matrizen, flächenerhaltend, viele Beispiele, Klassifikation von Kegeln mittels Hermite-Normalform	proSE	[HNP, §2.1] [HS, §0.3]	Jannes Siems
04.11.	Pick, Ehrhart Picks Formel für Dreiecke, für Polygone; Korollar: Ehrhart-Polynom, Reziprozität (brauchen Euler-Formel für 24)	proSE	[AZ, §10.3] [BR, §2.6]	Simon Treu
11.11.	kein Vortrag
18.11.	Kettenbrüche Approximation reeller Zahlen durch rationale	SE	[Sch, §6.1] [W, §§5,6]	Konstantin Jaehne
25.11.	reflexive Polygone, unimodulare Fächer zulässige Strecken, polare Streckenzüge; Fächer-Parameter berechnet Länge der polaren Kante	proSE	[HS, vor Satz 12] [HNP, 5.1.7, 5.1.8]	Barbara Schulzke
02.12.	Der Raum der phylogenetischen Bäume	extern		Lena Walter
09.12.	Klassifikation unimodularer Fächer unimodulare stellare Unterteilung, Existenz gemeinsamer Verfeinerung ggf. Klassifikation "minimaler" Fächer [Fulton §2.5/Ewald §V.6.6]	proSE	[HNP, 5.1.12]	Christian Haase
16.12.	12 12 folgt aus Fächersatz Korollar: Klassifikation reflexiver Polygone	proSE	[HNP, 5.1.9]	Philipp Schäfer
23.12.	Klassifikation von Polygonen mit unimodularen Ecken	SE	[8, §3.3.1-2]
23.12.	3-dimensional reflexiv, 24 braucht Euler-Formel	SE	[HNP, §5.1.2]
06.01.	Scottsche Ungleichung Beispiele (siehe auch Fig. 2.5 in [HNP]), P-in-a-box-Beweis	proSE	[HS, §2]
13.01.	adjungierte Polygone Definition Level, (durch Homogenität eindeutig bestimmt) Lemmata 8,9,10	proSE/SE	[HS, §3.1]
20.01.	Zwiebelsatz Lemma 11, Induktion; ggf. zweiter Beweis	proSE	[HS, §3.1]
27.01.	Gitterpunkte in Minkowskisummen Minkowskisumme, viele Beispiele (auch 3-dimensional)	proSE	[HNPS]	Maximilian Kertel
03.02.	torische Ideale quadratisch erzeugt	SE
10.02.

Erste Literatur

[DGH]	Dzambic, Gerbig, Haase Fastfood, quadratische Magie und Gitterpunkte pdf
[AZ]	Aigner, Ziegler Proofs from The Book Springer
[HNP]	Haase, Nill, Paffenholz Lattice Polytopes pdf
[dBCvKO]	de Berg, Cheong, van Kreveld, Overmars Computational Geometry: Algorithms and Applications http://www.cs.uu.nl/geobook/introduction.pdf
[Sco]	Scott On convex lattice polygons Bull. Austral. Math. Soc. 15(3), 395--399 (1976)
[HNPS]	Haase, Nill, Paffenholz, Santos Lattice Points in Minkowski Sums Electronic Journal of Combinatorics , 15:#N11, 2008
[HS]	Haase, Schicho Lattice Polygons and the number 2i+7 American Mathematical Monthly February: 151 - 165, 2009
[Sch]	Schrijver Theory of Linear and Integer Programming Wiley
[BR]	Beck, Robins Computing the Continuous Discretely Springer
[JT]	Joswig, Theobald Algorithmische Geometrie Vieweg
[PRV]	Poonen, Rodriguez-Villegas Lattice polygons and the number 12 Amer. Math. Monthly, 107(3):238--250, 2000
[8]	Bogart, Haase, Hering, Lorenz, Nill, Paffenholz, Rote, Santos, Schenck Finitely many smooth d-polytopes with n lattice points arXiv:1010.3887
[W]	Wolfart Skript Diophantische Approximationen http://www.math.uni-frankfurt.de/~wolfart/Lehre/Dioph.pdf