Aim of the talk: Let
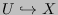 be a toroidal embedding with a
Cartier divisor
be a toroidal embedding with a
Cartier divisor  having support equal to
having support equal to
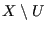 . Show that
the allowable modifications
. Show that
the allowable modifications 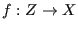 with
with 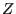 non-singular and
non-singular and
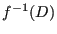 a reduced divisor correspond to certain decompositions of
the conical polyhedral complex attached to
a reduced divisor correspond to certain decompositions of
the conical polyhedral complex attached to
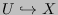 .
.
Details: In II, §2 state Theorem 9*- 12*. Prove as much of
Theorem 10* and 12* as possible.
N.N.
Christian Haase
2015-04-16